スカラー関数の勾配、grad、▽
力学的エネルギー保存則を論じるため保存場の知識が必要なのでしばらく物理数学のお勉強。ここへんは工高生には退屈なところだけどしばらくガマンのところ。
スカラー関数とは…
高校時代は多変数関数はやらなかったので、これを出すといきなりな感じはするけど大したことはない。
u(x,y,z)で表される関数のこと、例えば温度分布や気圧など。ある緯度、経度、標高における温度とか気圧などのようにひとつの値で示される関数のことである。これらの関数は途中で切れたり、折れ曲がったりしない、つまり階段的な値の変化はない範囲で定義されている。そうしないと途中で微分できなくなる。
力学においてはスカラー関数が保存場で質点にかかる力が次ぎような関係で結ばれる。
…(1)
によって導入されるスカラー関数U(x,y,z)のことを言う。このページは物理数学なのでFを力など具体的な物理量ではなく導き出されたベクトルのひとつとして話を進める。∂記号は偏微分の記号で∂U(x,y,z)/∂xというのは高校時代に習ったf(x)の導関数df(x)/dxと同じようにyとzを固定してxだけをわずかに動かしてUがどのくらい変化してみるというワケです。つまり
同様にyの偏微分は
同様にzの偏微分は
まとめると(1)式は最初x方向にΔx動かしてUの変化を見、次ぎにY方向にΔy動かしてUの変化を見、z方向にΔz動かしてUの変化を見るとうこと。
iはX軸に平行な大きさ1の単位ベクトルで、同様にjおよびkはY軸、Z軸に平行な単位ベクトルでそれらに係数を掛けることによって成分と元のベクトルを結びつけることができる。
ここでの係数はX軸は∂U/∂x、Y軸は∂U/∂y、Z軸は∂U/∂zとなります。ではこれらが結び付けられたベクトルは何を表すのかを見るのが今回の主たる課題だけど、そうした場合、簡単にするため特殊な例から考察し、一般化する方向が理解の早道。そこで∂U/∂xだけが有現値=aで∂U/∂y =0、∂U/∂z =0の場合。
これはUの値がX軸方向のみ変化し、Y軸、Z軸方向には変化しないことからU=costになる点を拾い上げるとX軸に垂直な面ができあがるだろう。そしてU=C1、U=C2、U=C3…なる点を見るとX軸に垂直な面がいくつもの層をなして見えるだろう。そこでC1とC2の面の距離をSとすればS=Δx、式(1)のFはX方向のベクトルF=-ai、でaが傾斜を表していることが分かる。
次ぎに∂U/∂z =0だが等値面がX軸とY軸の間の軸にある場合は図で示すと、
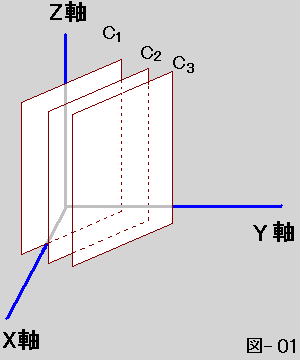 左のような図になる。ただし有限な広さに見えるが、左右上下につづいていることとする。この図を真上つまりZ軸と平行になるように見下ろすと下図のようになる。製図では平面図という。X軸に垂直な時と同じようにC2-C1=ΔUとすればa=ΔU/Sで分母のSはX軸となす角度をθとすればΔx=S/cosθとなる。Δy=S/sinθなので(1)の右辺カッコの中は
左のような図になる。ただし有限な広さに見えるが、左右上下につづいていることとする。この図を真上つまりZ軸と平行になるように見下ろすと下図のようになる。製図では平面図という。X軸に垂直な時と同じようにC2-C1=ΔUとすればa=ΔU/Sで分母のSはX軸となす角度をθとすればΔx=S/cosθとなる。Δy=S/sinθなので(1)の右辺カッコの中は
↑の平面図が↓
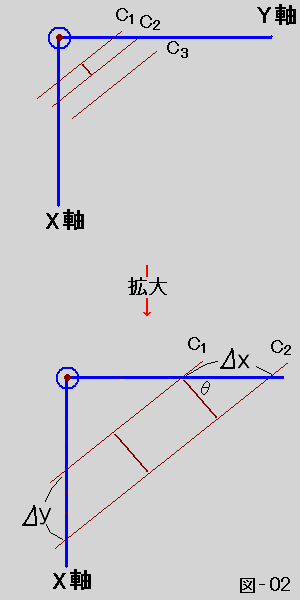 これはaが等値面C1と等値面C2の間の最短距離におけるUの変化で∂U/∂xはX軸、∂U/∂yはY軸への成分である。(1)の右辺カッコの中はUの最大勾配である。次はZ軸でも平行でない場合つまり任意の角度でも同様に計算できるが複雑な計算必要。もうすこし簡単に証明できる方法もある。むしろ多くの物理数学の教科書に出ているやり方で、それは任意の方向でのUの変化は
これはaが等値面C1と等値面C2の間の最短距離におけるUの変化で∂U/∂xはX軸、∂U/∂yはY軸への成分である。(1)の右辺カッコの中はUの最大勾配である。次はZ軸でも平行でない場合つまり任意の角度でも同様に計算できるが複雑な計算必要。もうすこし簡単に証明できる方法もある。むしろ多くの物理数学の教科書に出ているやり方で、それは任意の方向でのUの変化は
で与えられる。▽(ナブラ)を使えば
となる。△rの方向を等値面に取れば△U=0なので▽Uと△rの内積が0なので▽Uと等値面は垂直だと分かる。このことから等値面同士の最短距離との勾配、傾斜を表している。